8 Linære modeller

I litteraturen skelner man i analyse af et kvantitativt outcome (f.eks. vitamin D) mellem

ANOVA - de forklarende variable er kategoriske (kvalitative/faktorer)
- one-way én forklarende variabel
- two-way to forklarende variable
- multi-way 3+ forklarende variable
regression - de forklarende variable er kvantitative
- simpel (emne uge 4)
- multipel
ANCOVA - én kvantitativ og én kategorisk (emne uge 5)
generel lineær model / multipel regression / multivariabel lineær model - blanding af kvantitative og kvalitative (emne uge 6)

I bund og grund er de alle specialtilfælde af den samme klasse af modeller - den generelle lineære model. I SPSS kan vi bruge menuen Analyze/General Linear Model/Univariate til alle disse analyser, så der bliver meget genbrug …

8.1 One-way ANOVA

Eksempel: Vitamin D (uge 2)

Her kan benyttes

Analyze/Compare Means/One-Way ANOVA.
- Fordele: kan lave Welch test i tilfælde af uens varianser
- Ulemper: Giver kun overordnet test for association og ikke parameterestimater og er i praksis derfor ret ubrugelig.
- Fremgangsmåde: Sæt responsvariablen (vitd) i Dependent List, den forklarende variabel (country) i Factor
Analyze/General Linear Model/Univariate.
- Fordele: er meget fleksibel, og kan klare generelle lineære modeller (til og med uge 7)
- Ulemper: lidt mere indviklet opsætning
- Fremgangsmåde: Sæt responsvariablen (vitd) i Dependent Variable og den forklarende variabel (country) i Fixed Factor(s). Under Options afkrydses Parameter estimates for at sikre, at der kommer parameterestimater i output.

Vi vil generelt benytte tilgang 2.

8.2 Two-way ANOVA

Eksempel: Vitamin D (uge 2)

Som one-way ANOVA, alle forklarende variable sættes i Fixed Factor(s). Derefter skal modellen ‘bygges’. Det gøres via knappen Model, hvor de to variable (i feltet ‘Factors & Covariates’) markeres, under Build Terms skal der stå Main effects, klik på pilen for at overføre variablene til Model. Dermed får man en model, hvor de to variable indgår som forklarende variable.

Interaktion:

Til at teste om der er interaktion: Efter de forklarende variable er sat i Fixed Factor(s) benyttes knappen Model, vælg Build Terms, markér de to variable du ønsker i interaktionen. Klik dem over i Model-feltet mens Build Terms står på Main Effects, derefter klikkes de over mens Build Terms står på Interaction. I Model-feltet skulle du nu gerne have tre linjer hvor disse variable indgår - hver for sig og med en stjerne imellem (f.eks. country, sol, country*sol, jvf slides uge 2).
til at estimere effekten af country i en model med interaktion skal i Model-feltet kun være: sol og country*sol. Dette gøres ved at markere country i Model-feltet og klikke den væk med pilen under Build Terms (således at der nu kun står sol og country*sol i Model-feltet).
til at estimere effekten af sol i en model med interaktion skal i Model-feltet kun være: country og country*sol. Dette gøres ved at markere sol i Model-feltet og klikke den væk med pilen under Build Terms (således at der nu kun står country og country*sol i Model-feltet).

8.3 Korrektion for multipel testning

Dette kan gøres via Analyze/General Linear Model/Univariate som beskrevet i one-way ANOVA (kap 8.1). Benyt knappen Post Hoc og sæt flueben ved f.eks. Tukey eller Games-Howell.

8.4 Lineær regression

8.4.1 Simpel lineær regression

Simpel lineær regression er en retningsbestemt relation mellem to kvantitative (kontinuerte) variable. Altså, kaldes en lineær regression simpel når vi har et kvantitativ outcome og én forklarende kvantitativ variabel.

Når man ønsker at lave en simpel lineær regression kan dette gøres ved 2 forskellige måder i SPSS: Man kan benytte menuen Analyze/General Linear Model/Univariate eller fremgangsmåden i Analyze/Regression/Linear. Som beskrevet i introduktionen til dette kapitel 8, benyttes oftest Univariate, da vi her kan lave alle de forskellige typer af lineære modeller, men Linear-fremgangsmåden kan også bruges til at udføre en simpel lineær regression.

Ved brug af Linear:
- Når vi benytter menuen Analyze/Regression/Linear til at lave en simpel lineær regression, skal den afhængige variabel (outcome) hives over i Dependent-boksen og den forklarende variabel i Independent(s)-boksen. Hernæst afkrydses i Statistics Confidence intervals, som ved default er valgt til det sædvanlige 95% CI. I menuen Save kan prædikterede værdier (Predicted Values) og residualer afkrydses (Residuals) , som vi gerne vil bruge til modelkontrol, se kapitel om modelkontrol 8.8. Når modellen køres, altså når der trykkes Ok, ses parameterestimaterne for modellen i Coefficients-tabellen i output.
  Estimatet for spredningen omkring regressionslinien ses i Model Summary-tabellen under Std. Error of the Estimate.
Ved brug af Univariate (som vi generelt bruger i SPSS når vi ønsker at arbejde med lineære modeller):
- Når vi benytter menuen Analyze/General Linear Model/Univariate til at lave en simpel lineær regression, hives den afhængige variabel (outcome) over i Dependent Variable-boksen, og den forklarende variabel i Covariate(s)-boksen (NB: Fordi den forklarende variabel er kvantitativ/kontinuert benyttes Covariate(s)-boksen). I Options afkrydses Parameter estimates for at sikre, at der kommer parameterestimater med i output. I menuen Save kan prædikterede værdier (Predicted Values) og residualer afkrydses (Residuals) , som vi gerne vil bruge til modelkontrol, se kapitel om modelkontrol 8.8. Når modellen køres, altså når der trykkes Ok, ses parameterestimaterne for modellen i Parameter Estimates-tabellen i output.
  Estimatet for spredningen omkring regressionslinien finder man som kvadratroden af den størrelse, som står under Error i søjlen Mean square i Test of Between-Subjects Effects-tabellen.

8.4.2 Forventet værdi for specifikke værdier af kovariaten

I SPSS kan man finde et estimat, med tilhørende usikkerhed (95% CI), for den forventede værdi af en afhængige variabel, for specifikke værdier af en forklarende variabel. Dette gør vi ved at “snyde” SPSS til at tro, at det er interceptet.

Følgende eksempel vil tage udgangspunkt i eksemplet fra uge 2 med IQ og lungefunktion for Vietnam veteranerne (datasæt med navn viet.sav) .

Vil vi eksempelvis beregne den forventede værdi af sammentrækningsevne for personer med IQ på 100, flytter vi nulpunktet hen i 100. Dette gør vi ved at lave en ny X-variabel, der er defineret ved IQ minus 10. Vi laver altså en ny variabel vi kalder iq100. Dette gør vi ved at bruge menuen Transform/Compute Variable… hvor vi skriver iq100 i feltet for Target Variable, og så definerer vi variablen i Numeric Expression-feltet, hvor vi hiver variablen iq over og trækker 100 fra. Vi laver altså følgende variabel: iq100=iq-100. Herefter gentages den lineære regression med iq100 som forklarende variabel i stedet for iq. Interceptet i outputtet for denne regression vil altså angive den forventede værdi af FEV1 med 95% CI for personer med en IQ på 100.

Man kan også forsøge at aflæse værdierne ud fra scatterplot med indtegnet regressionslinje og punktvise konfidensgrænser. Vejledning til hvordan et scatterplot og konfidensgrænser laves i SPSS, finder du i kap 2.4.3. Når du har indlagt konfidensgrænser kan du for IQ=100 aflæse de relevante oplysninger. Du finder nok ud af, at vil man have et præcist resultat for den forventede værdi af sammentrækningsevne for personer med en IQ på 100, er metoden hvor vi laver regressionen med en ny variabel for IQ,iq100, mere præcis…

(Avanceret: Alternativt kan man tilføje en ekstra observation (linje) i sit datasæt, hvor man sætter iq=100 og outcome FEV1 til manglende (FEV1=.). Man kan nu vælge at gemme prædikterede værdier, når man kører sin linære regression via Analyze/General Linear Model/Univariate (se kap 8.8). Ud for den fiktive observation, med manglende outcome, kan man nu aflæse prædiktionen i variablen PRE_1. Men her får vi så ikke noget CI med og det vil vi jo gerne have …).

8.4.3 Kovariansanalyse (ANCOVA)

Når vi har netop en kvantitativ og en kategorisk kovariat kalder vi vores analyse af et kvantitativt outcome en kovariansanalyse eller ANCOVA. Lig de andre lineære modeller i dette afsnit benytter vi os af menuen Analyze/General Linear Model/Univariate. Her hives den afhængige variabel (outcome) over i Dependent Variable- boksen, den kvantitative kovariat i Covariate(s)- boksen & den kategoriske kovariat i Fixed Factor(s)- boksen.I Options afkrydses Parameter Estimatesfor at sikre, at der kommer parameterestimater med i output.

8.4.4 Interaktion

Når en lineær model laves ved brug af menuen Analyze/General Linear Model/Univariate kan en interaktion tilføjes til modellen ved at klikke på Model.... Her vælges Build terms i Specify model-boksen. Når du har afkrydset Build terms bliver dine variable aktive i Factors & Covariates-boksen til venstre. Ønsker du at tilføje en interaktion til din model markerer du de to variable du ønsker at lave interaktionen imellem, ændrer til at der står Interaction i Build Term(s)-boksen i midten og hiver interaktionen over i Model-boksen til højre ved at bruge pilen. SPSS illustrerer et interaktionsled med en stjerne imellem variablene. Du skal herefter huske at tilføje alle variablene du ønsker i din model i Model-boksen til højre, altså ikke kun interaktionsleddet. Du afslutter herefter ved at klikke Continue. Husk også at afkrydse Parameter Estimates under Options. Kør modellen ved OK - knappen.

8.5 Multipel regressionsanalyse

Når man ønsker at lave en regressionsanalyse af et kvantitativt outcome hvor kovariaterne er både kvantitative og kategoriske, kalder vi det for multipel regressionsanalyse eller for en generel lineær model (GLM). Til en sådan analyse vil vi benytte menuen Analyze/General Linear Model/Univariate, som tidligere. Når vi ønsker at lave multipel regressionsanalyse hives den afhængige variabel (outcome) over i Dependent Variable-boksen, og de kvantitative forklarende variable over i Covariate(s)-boksen, og de kategoriske forklarende variable over i Fixed Factor(s)-boksen. I Options afkrydses Parameter estimates for at sikre, at der kommer parameterestimater med i output. I menuen Save kan prædikterede værdier (Predicted Values) og residualer afkrydses (Residuals), så der kan laves modelkontrol, se kapitel om modelkontrol 8.8. Parameterestimaterne ses i Parameter Estimates-tabellen i output. Interaktioner tilføjes ved brug af stjerneled, se kapitel 8.4.4.

Ønsker man at lave en regressionsanalyse af et kvantitativt outcome med to eller flere kvantitative kovariater kan en sådan multipel lineær regression laves ved metoden som ovenfor - Analyze/General Linear Model/Univariate - men analysen kan også laves ved brug af menuen Analyze/Regression/Linear. Ved brug af Linear-metoden hives alle de kvantitative kovariater over i Independent(s)-boksen.

For mere information vedrørende forskellen på de to metoder, se kapitel 8.4.1.

8.6 Variabelselektion

Vi fraråder i det hele taget at benytte variabelselektionsprocedurer….

Når vi har mange mulige kovariater i spil og gerne vil have reduceret dette antal uden at have en holdning til, hvilke variable der bør være med i modellen, vælger nogle at lave automatisk variabelselektion. Dette kan gøres på flere måder:

Backwards elimination: Fjerner i hvert skridt den mindst signifikante
Forwards selection: Tilføjer i hvert skridt den mest signifikante
Hybrid mellem forwards og backwards

I SPSS foretages variabelselektion ved at klikke på Method:-boksen i regressionsopsætningen, og der kan nu skiftes fra Enter (“den kontrollerede og anbefalede metode”) til Backward eller Forward.

8.7 Prædiktion til brug for illustrationer

Hvis man gerne vil illustrere de predikterede værdier for en regressionsmodel grafisk kan man benytte følgende metode:

Nedenstående metode tager udgangspunkt i en regressionsmodel med et kvantitativt outcome og 2 kovariater, hvor den ene kovariat holdes fast.

1) Tilføj de fiktive personer, du gerne vil prediktere outcome for. Tilføj personerne til datasættet, med manglende værdier af outcome (altså missing-value for outcome), men med de værdier af kovariaterne som du gerne vil lave prædiktioner for.
2) Lav en kolonne, kaldet f.eks. ny, som skal have værdien 0 for alle de oprindelige observationer, men 1 for de nye fiktive observationer.
3) Estimer nu i samme model som før i det udbyggede datasæt og gem de predikterede værdier (nu hedder de sikkert PRE_2, fordi du har gemt nogen tidligere fra din oprindelige model).
4) Hvis du har log-transformeret: Transformer de predikterede værdier tilbage til oprindelig skala ved at benytte menuen Tranform/Compute Variable, skriv predikteret i Target Variable-boksen og tilbagetransformer i Numeric Expression-boksen.

Selve figurerne laves ved herefter at begrænse dit datasæt til de fiktive personer/observationer ved at benytte menuen Data/Select Cases vælge If condition is satisfied/If.. og skrive ny=1 (se punkt 2)). Vælg nu Graphs/Chart Builder og herefter Line, hvor du skal vælge dét ikon der viser multiple lines. I den fremkomne boks trækkes PRE_2 (eller hvad dine nye predikterede værdier hedder) over på Y-aksen, den ene kovariat på X-aksen og den anden i Set color-boksen oppe i højre hjørne.

NB: Vær opmærksom på om du arbejder med logaritme-transformeret data, i så fald kan du også vælge at trække din tilbagetransformerede variabel for de predikterede værdier (se punkt 4)) over på Y-aksen i stedet for. Arbejder du desuden med en logaritme-transformeret kovariat, kan du ligledes plotte den tilbagetransformerede version på X-aksen i stedet for den transformerede.

8.8 Modelkontrol

Modelkontrol laves ved brug af prædikterede værdier og residualer. Når vi laver analysen via Analyze/General Linear Model/Univariate kan vi gemme disse som nye variable i vores datasæt. Benyt Save-knappen og vælg Unstandardized under Predicted Values og f.eks. Studentized under Residuals. Derved får man to nye variable i sit datasæt: PRE_1 (prædikterede værdier) og SRE_1 (residualer). Det er disse variable vi vil bruge til modelkontrol.

8.8.1 Normalfordeling

QQ-plot af residualerne SRE_1, se kap 2.3.

Histogram af residualerne med overlejret normalfordeling, se SPSS intro on histograms

8.8.2 Varianshomogenitet

Her skal vi plotte residualer SRE_1 mod de prædikterede (fittede værdier) PRE_1. Det gøres via Graphs/Chart Builder, vælg første plotmulighed i Scatter/Dot, og sæt PRE_1 på x-aksen, SRE_1 på y-aksen.

Man kan vælge at indlægge en vandret linje i 0 ved at dobbeltkligge på sin graf, så den bliver aktiv for redigering, og hernæst højreklikke og vælge Add Y Axis Reference Line. Når man vælger denne funktion dukker en ny boks op, hvor man i Position-boksen skriver 0, og hernæst lægger linjen ind i plottet ved at vælge Apply. En sådan linje kan hjælpe dig med at vurdere mulige mønstre i plottet. Ligeledes kan man lægge en udglattet Loess-kurve ind i plottet, ved at klikke Add fit line at total og hernæst vælge Loess i Fit Method-menuen. Husk at afslutte med Apply.

Varianshomogenitet kan også tjekkes ved at plotte kvadratroden af numerisk værdi af normerede residualer mod de prædikterede værdier. De normerede residualer hedder SRE_1, og for at definere kvadratroden af de numeriske residualer definerer vi en ny variabel ved brug af menuen Transform/Compute variable…. I Target Variable-boksen skriver vi sqrtres og definerer variablen i Numeric Expression-boksen ved at indføre sqrt(abs(SRE_1)). Herefter fremstilles figurerne som sædvanligt via menuen Graph/Chart Builder.

8.8.3 Linearitet

Kun relevant for lineær regression. Her plottes residualerne SRE_1 mod kovariaten (som er kvantitativ). Dette gøres via menuen Graphs/Chart Builder, og hernæst Scatter/Dot, hvor kovariaten sættes på x-aksen og SRE_1 på y-aksen. Her kan du som beskrevet ovenfor i afsnittet om varianshomogenitet vælge at lægge en vandret linje i 0 ind i din graf eller en Loess-kurve.

8.9 Diagnostics

8.9.1 Cooks afstand

Et plot af Cooks afstand kan bruges til at vurdere inflydelsesrige observationer. For at kunne plotte Cooks afstand skal vi i menuen Save, når vi laver regressionen, afkrydse Cook’s i Distances-boksen. Når vi herefter laver regressionen, får vi genereret en variabel i datasættet for denne størrelse: COO_1. Variablen COO_1kan efterfølgende benyttes på forskellig vis. Man kan eksempelvis plotte COO_1 mod den forklarende variabel i ens analyse i et scatterplot, for at få et indtryk af indflydelsesrige observationer.

Hvis én (eller flere) observationer ses at stikke ud i plottet, kan vi ved at dobbeltklikke på plottet og gøre det aktivt for redigering, få information om observationen. Markér observationen - der vil fremkomme gule ringe om alle observationerne -, højreklik herefter og vælg Show Data Labels. Vi kan nu se observationens nummer, så vi kan kigge nærmere på den i datasættet.

8.9.2 Influence

Influence er Cook’s afstand spaltet ud på de enkelte estimerede parametre (dvs. intercept og hældninger). Dette laves ved at afkrydse i Standardized DfBeta(s) (og evt. også DfBeta(s)) under Influence Statistics i regressions-menuen Save. Herefter benyttes menuen Graph/Chart builder/Scatter/Dot som tidligere.

8.9.3 Kollinearitet

I en multipel regressionsmodel er der en risiko for, at der er kollinearitet mellem nogle af kovariaterne. For at undersøge kollinearitet går man i regressionsopsætningen Analyze/Regression/Linear ind under Statistics og afkrydser Collinearity diagnostics.

8.10 Splines

Hvis en ikke-lineær sammenhæng ikke kan transformeres til linearitet (f.eks. ved log-transformation af kovariaten) kan man benytte spline-funktioner. Her findes forskellige varianter, den simpleste, som præsenteres her, er lineære splines. Her skæres en kurve op i stykkevis lineære bidder. Fordelene ved at bruge lineære splines i forhold til andre typer af splines er, at vi får en model som er let at rapportere - vi kan give en hældning i hvert af intervallerne.

I eksemplet med væksthormon (kapitel 1.14) som funktion af alder gennemgået i uge 7, lavede vi sammenhængen stykkevis lineær i intervaller < 10, 10-12, 12-13, 13-15, > 15 år, dvs kurven knækker ved alder 10, 12, 13 og 15 (svært at se knæk ved 10 og 12 år):

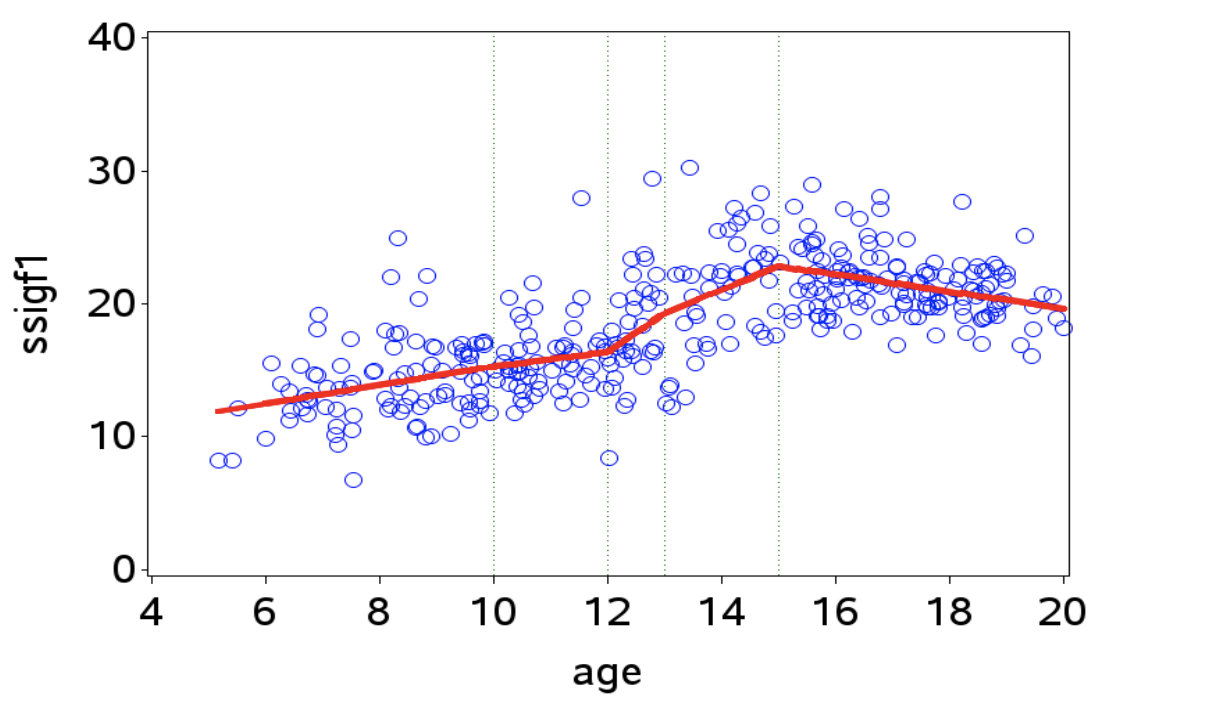
I SPSS fittes en sådan kurve ved først at tilføje en ekstra kovariat (spline-variabel) for hvert knækpunkt i modellen. Benyt menuen Transform/Compute variable, hvor navnet på den nye variabel defineres i Target Variable-feltet, og selve variablen defineres i Numeric Expression-feltet.

extra_age10=max(age-10,0)
extra_age12=max(age-12,0)
extra_age13=max(age-13,0)
extra_age15=max(age-15,0)

Fit herefter en model med age og disse 4 ekstra kovariater. Benyt menuen Analyze/Regression/Linear, og sæt ssigf1 (kvadratrodstransformeret sigf1) i Dependent Variable-boksen, og de forklarende variable (de 4 spline-variable og _age) i Independent(s):- boksen. I “Statistics” afkrydses “Estimates” og “Confidence Intervals” for at sikre, at der kommer parameterestimater og 95% CI med i output.

Fortolkningen af spline-variablene er her: koefficienten til extra_age1 angiver forskellen i hældning i intervallet 10-12 ifht < 10, extra_age12 angiver forskellen i hældning i intervallet 12-13 ifht 10-12 etc. Er alle disse forskelle i hældninger 0, dvs ingen effekt af splinevariablene, har vi kun age tilbage - og dermed linearitet.

Hvis vi gerne vil finde hældningen i hvert aldersinterval fremfor forskellen i hældninger mellem intervallerne, fortæller og viser Lene i slides hvordan disse kan fås som kombination af estimater, men også hvordan dette kan laves ved at bestemme og bruge nye spline-variable som kovariater:

Alternativ parametrisering af lineære splines:

I stedet for at få forskelle i hældninger frem, kan man bede SPSS bestemme hældningen i hvert interval. Det vil vi gøre, hvis vi skal rapportere en model med lineære splines.

Definér nye variable ved igen at bruge menuen Transform/Compute variable, men definér nu variablene ud fra spline-variablene ovenfor således:

ny_age=min(age`,10)
ny_age10=min(extra_age10,2)
ny_age12=min(extra_age12,1)
ny_age13=min(extra_age13,2)
ny_age15=extra_age15

Tallene 2, 1 og 2 benyttet i min-funktionerne angiver længden af intervallerne (her 12-10=2, 13-12=1, 15-13=2).

Fit herefter en model med disse fem nye kovariater, i analogi med den beskrevne fremgangsmåde ovenfor. Nu fortolkes estimater som hældningerne i de successive aldersintervaller.

8.11 Test af flere parametre

Eksempel: Vitamin d uge 7, den generelle lineære model.

I eksemplet gennemgået i forelæsningerne ønsker vi at teste, om der samlet set er effekt af bmi, sunexp og lvitdintake på log-transformeret vitamin D (lvitd), justeret for country. Vi spørger altså om vi kan udelade disse tre variable på én gang og kun beholde country i modellen. Dette kan gøres ved et F test med 4 frihedsgrader (1 for bmi, 2 for sunexp og 1 for lvitdintake).

Dette er dog ikke helt nemt at gøre i SPSS. Hvis alle kovariater var kvantitative (altså i en multipel regressionsanalyse) kan man i menuen Analyze/Regression/Linear definere flere modeller på en gang og få dem sammenlignet med et F-test. Når vi som her også har kategoriske kovariater, benytter vi normalt menuen Analyze/General Linear Model/Univariate, og denne opsætning tillader ikke definition af flere modeller på en gang.

Analysen skal derfor laves vha Analyze/Regression/Linear. Herer man nødt til at lave sine kategoriske variable om til dummy-variable, f.eks. skal country så blive til 3 dummy-variable:

landDK=1 hvis country=1, 0 ellers
landFI=1 hvis country=2, 0 ellers
landEI=1 hvis country=4, 0 ellers

Disse 3 dummy-variable laves vha menuen Transform/Recode into Different Variables. Vælger man som her dummy-variable for DK, FI og EI, bliver SF som det manglende land referencen. Prøv evt at køre en model med country-variablen og derefter med de 3 dummy-variable i stedet og se at du får præcis det samme. Tilsvarende skal laves to dummy-variable for sunexp-variablen.

Nu benyttes Analyze/Regression/Linear. Sæt vitd i Dependent. De variable vi ønsker at beholde i modellen (her landDK, landFI og landEI) sættes i Independent(s). I feltet Method lige under vælges Enter. Her har du defineret Block 1 af 2, klik på Next for at komme til Block 2. Her sætter du variable svarende til den store model ind (dvs igen landDK, landFI og landEI samt age, bmi og de to dummy-variable du har defineret for sunexp).
I Statistics vælges Estimates, Confidence Intervals, Model fit og R squared change. Du får nu i output en tabel med navn Model Summary, som har to linjer. P-værdien for sammenligning af de to modeller aflæser du i linje 2 (Model 2) i sidste søjle under “Sig. F. Change”, her bliver det et test med 4 frihedsgrader (1 for bmi, 1 for age og 2 for de to dummy-variable hørende til sunexp). Er denne under 5% kan du ikke fjerne de 3 variable fra modellen, er den over 5% kan du tillade dig at tage dem alle 3 ud på en gang.