5 Lineære modeller
I litteraturen skelner man i analyse af et kvantitativt outcome (f.eks. vitamin D) mellem
- ANOVA - de forklarende variable er kategoriske (kvalitative/faktorer)
- one-way én forklarende variabel
- two-way to forklarende variable
- multi-way 3+ forklarende variable
- one-way én forklarende variabel
- regression - de forklarende variable er kvantitative
- simpel (emne uge 4)
- multipel
- ANCOVA - én kvantitativ og én kategorisk (emne uge 5)
- generel lineær model / multipel regression / multivariabel lineær model - blanding af kvantitative og kvalitative (emne uge 6)
I bund og grund er de alle specialtilfælde af den samme klasse af modeller - den generelle lineære model. I R er der derfor kun en funktion, vi bruger til alle disse typer af analyser, så nu bliver der ret meget genbrug …
Bemærk at du ikke kan køre kommandoerne i dette afsnit, hvor jeg blot giver en oversigt over de kommandoer vi bruger til lineære modeller. Kommandoer fra afsnit 5.1 kan du prøve at køre.
Til at lave analysen benytter vi lm() (Linear Model). Vi specificerer modellen ved formel notation. På venstre side af en ~ sætter vi outcome / respons (f.eks. vitd), på højre side en eller flere forklarende variable adskilt af +-er. Dertil et data-argument. Dvs syntaks a la
model <- lm( respons ~ forklarende1 + forklarende2, data=d )Interaktioner specificeres ved:
forklarende1*forklarende2- benyttes til at teste for interaktionforklarende1 + forklarende1:forklarende2- benyttes til at beskrive en effekt med interaktion (her rapporteres effekten afforklarende2for hvert niveau afforklarende1). Se forelæsninger / script uge 2
Vi får desværre ikke så meget information ud af lm() men skal selv trække det hele ud. Hertil benytter vi igen og igen funktionerne:
plot( model )
plot( model, which=1) # for at bede om plot nr 1 af 6 mulige (1:6)
coef( model ) # estimerede koefficienter
summary( model ) # estimerede koefficienter + p-værdier
confint( model ) # konfidensintervaller for koefficienterneOverordnede p-værdier
I forbindelse med kvalitative forklarende variable (faktorer) benytter vi flere forskellige funktioner til at bestemme p-værdier. Afhængigt af hvad vi spørger til, skal vi benytte forskellige (og det tager tid at lære hvilken, så forvent forvirring i starten indtil du har helt styr på at aflæse output …). Vi tager den til øvelserne
aov( model ) # Analysis Of Variance, overordnet p-værdi
# Bør kun benyttes i forb med Tukey-korrektion,
# da p-værdierne afhænger af hvilken rækkefølge
# man har sat de forklarende variable ind
# (aflæs kun nederste p-værdi hvis flere
# forklarende variable
# i model)
anova( model ) # Overordnede p-værdier + test for interaktion
# Afhænger af rækkefølge af forklarende variable
# (aflæs kun nederste p-værdi hvis flere forklarende variable
# i model)
drop1( model, test='F' ) # Overordnede p-værdier (afhænger ikke af den rækkefølge
# variablene i modellen står på men kan ikke benyttes til
# test for interaktion.Prædiktion
Først skal man definere de værdier man vil prædiktere for i en ny dataframe, dernæst prædikterer (pred()) man ud fra en model. Syntaks a la (men se fx forelæsningsscript uge 2)
# prædiktion for danske og irske kvinder på alder 65
# Kræver at vi har fittet en model med forklarende variable
# country og age
nyedata <- data.frame( country=c('DK','EI'), age=65 )
pred( model, nyedata)Se mere om prædiktion i kap 5.8.
Modelkontrol
Vi ønsker altid at kontrollere følgende:
- Normalfordeling af residualer ved hjælp af et qq-plot (eventuelt et histogram)
- Varianshomogenitet - residualer plottet mod fittede (=prædikterede) værdier
- Linearitet hvis vi har kvantitative forklarende variable
Se hvordan i kapitel om modelkontrol nedenfor.
5.1 One-way ANOVA
Her har vi én forklarende kvalitativ (factor) variabel:
model.oneway <- lm( vitd ~ country, data=vit )Et overordnet test for association kan vi få med
drop1( model.oneway, test="F" )Estimerede koefficienter incl p-værdier for de individuelle sammenligninger får vi med
summary( model.oneway )Konfidensintervaller med
confint( model.oneway )5.1.1 Test for ens varianser
I en one-way ANOVA kan vi teste om variansen er ens i alle grupper:
Enten med Bartlett’s test
bartlett.test( vitd ~ country, data=vit )eller Levene’s test (jeg plejer at benytte Levene):
install.packages("lawstat") # kør kun én gang
library(lawstat)
levene.test( vit$vitd, vit$country)Bemærk at levene.test() ikke benytter formelnotation (~) men komma.
5.1.2 Tukey korrektion for multiple sammenligninger
aov.oneway <- aov( model.oneway )
TukeyHSD( aov.oneway )5.2 Two-way ANOVA
model.twoway <- lm( vitd ~ country + sol, data=vit )Det er ligegyldigt hvilken rækkefølge man sætter de forklarende variable ind.
Vi benytter samme funktioner som ovenfor, f.eks. drop1() for at få overordnede p-værdier :
drop1( model.twoway, test='F')Find selv estimerede koefficienter incl p-værdier og CI som beskrevet i kapitel 5.1 om one-way ANOVA.
5.3 Simpel lineær regression
Her har vi én forklarende kvantitativ (numerisk) variabel.
Eksempel: Vietnam veteraner, IQ og lungefunktion.
model.linreg <- lm( FEV1 ~ iq, data = viet )Estimerede koefficienter, p-værdier og CI for estimater findes med summary og confint:
summary(model.linreg)
confint(model.linreg)Plot af den estimerede regressionslinje fås ved at tilføje regressionslinjen med abline():
plot( viet$FEV1 ~ viet$iq, col = "blue")
abline(model.linreg, col = "red", lwd = 2)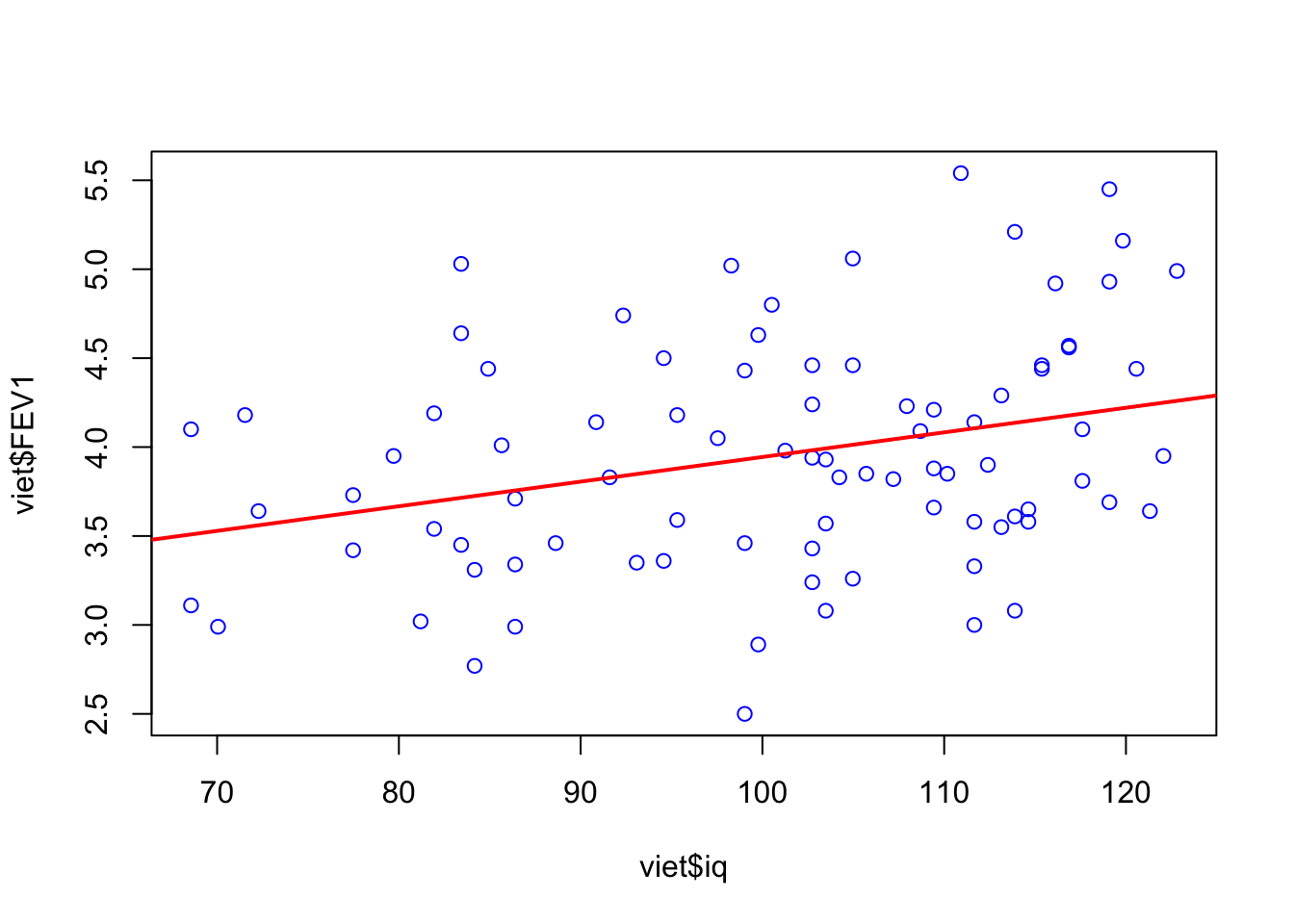
5.4 Kollinearitet
Eksempel: Lungefunktion og cystisk fibrose (uge 6)
I en multipel regressionsmodel er der en risiko for, at der er kollinearitet mellem nogle af kovariaterne.
For at undersøge kollinearitet benyttes Variace Inflation Factor (VIF), Tolerance (1/VIF) og standardiserede koefficienter.
VIF og tolerance bestemmes vha. vif-funktionen i car-pakken:
Her benytter vi modellen med alle de mulige kovariater, fuld:
install.packages("car")
library(car)fuld = lm( pemax ~ age+factor(sex)+height+weight+bmp+fev1+rv+frc+tlc, data=pemax )
# VIF (større end 5-10 er problematisk)
VIF <- vif( fuld )
VIF age factor(sex) height weight bmp fev1
21.830 2.269 13.955 47.781 7.116 5.420
rv frc tlc
10.538 17.143 2.660 # tolerance (mindre end 0.1-0.2 er problematisk)
tolerance <- 1 / vif( fuld)
tolerance age factor(sex) height weight bmp fev1
0.04581 0.44064 0.07166 0.02093 0.14053 0.18452
rv frc tlc
0.09489 0.05833 0.37594 De standardiserede koeffienter findes fra en model, hvor alle kovariater er skaleret til at have middelværdi 0 og standard afvigelse 1. Alle kovariater kan let skaleres med funktionen scale(), hvor vi sætter center=TRUE for at få middelværdi 0 og scale=TRUE for at få standard afvigelse 1.
Her laver vi os et nyt datasæt kun bestående af de skalerede kovariater (variable nummer 2-10) og benytter derefter disse som forklarende variable (lettere end at sidde og definere et hav af nye skalerede variable i hånden med kode a la pemax$scaled_age <- scale(pemax$age, center=T, scale=T) for derefter at benytte disse nye variable i modellen):
ny.x <- scale( pemax[ , c(2:10)], center=TRUE, scale = TRUE )
fuld.ny <- lm( pemax$pemax ~ ny.x )Vi kan herefter bestemme de standardiserede koefficienter ved at plukke estimat nr 2-10 ud af modellen med coef og dividere med SD af outcome:
stand.beta <- coef(fuld.ny)[2:10] / sd(pemax$pemax)
stand.beta ny.xage ny.xsex ny.xheight ny.xweight ny.xbmp ny.xfev1 ny.xrv
-0.38460 -0.05662 -0.28694 1.60200 -0.62651 0.36190 0.50671
ny.xfrc ny.xtlc
-0.40327 0.09571 Vi kan evt vælge at samle de fundne størrelser i en tabel med cbind:
cbind( stand.beta, tolerance, VIF )Vi ser, at nogle af kovariaterne har en høj VIF indikerende kollinearitet.
5.5 Variabelselektion
Vi fraråder i det hele taget at benytte variabelselektionsprocedurer….
Når vi har mange mulige kovariater i spil og gerne vil have reduceret dette antal uden at have en holdning til, hvilke variable der bør være med i modellen, vælger nogle at lave automatisk variabelselektion. Dette kan gøres på flere måder:
- Backwards elimination: Fjerner i hvert skridt den mindst signifikante
- Forwards selection: Tilføjer i hvert skridt den mest signifikante
- Hybrid mellem forwards og backwards
Med funktionen step er det muligt at lave alle tre typer variabel-selektion ved at specificere direction. Ved backwards elimination angiver vi den største model som startmodellen, og ved forward elimination angives den simpleste model som startmodellen.
# Backwards elimination: Fjerner i hvert skridt den mindst signifikante
step(fuld, direction = "backward", trace=T)
# Forwards selection: Tilføjer i hvert skridt den mest signifikante
tom <- lm( pemax ~ 1, data=pemax)
step(tom, direction = "forward", scope=list(upper=fuld,lower=tom), trace=T)
# Hybrid mellem forwards og backwards
step(tom, direction = "both", scope = list(upper=fuld,lower=tom), trace=T)5.6 Modelkontrol
Vi kontrollerer altid:
- Normalfordeling af residualer ved qq-plot (eventuelt et histogram)
- Varianshomogenitet - residualer plottet mod fittede (=prædikterede) værdier
- Linearitet hvis vi har kvantitative forklarende variable
Disse plots kan først laves, når vi har ‘fittet’ modellen med lm() og gemt den i et objekt (f.eks. med navn model.twoway).
Plots til modelkontrol er lette af lave med plot() på et model-objekt, hvor man kan angive which=1,...,6 for at indikere, hvilket plot af de 6 mulige, man ønsker.
5.6.1 QQ-plot (normalfordeling?)
plot( model.twoway, which=2)5.6.2 Residualplot (varianshomogenitet?)
Plot af residualer mod fittede(=prædikterede) værdier.
plot( model.twoway, which=1)Vi kan også plotte kvadratrod af numerisk værdi af normerede residualer:
plot(model.twoway, which = 3, cex.lab = 1.5)5.6.3 Linearitet
Eksempel: Vietnam veteraner, IQ og lungefunktion.
Kontrol af linearitet for kvantitativ forklarende variabel (her iq, i modellen model.linreg (kap 5.3):
scatter.smooth( resid(model.linreg) ~ viet$iq, col = "blue")
abline(0, 0, col = "red", lty = 2)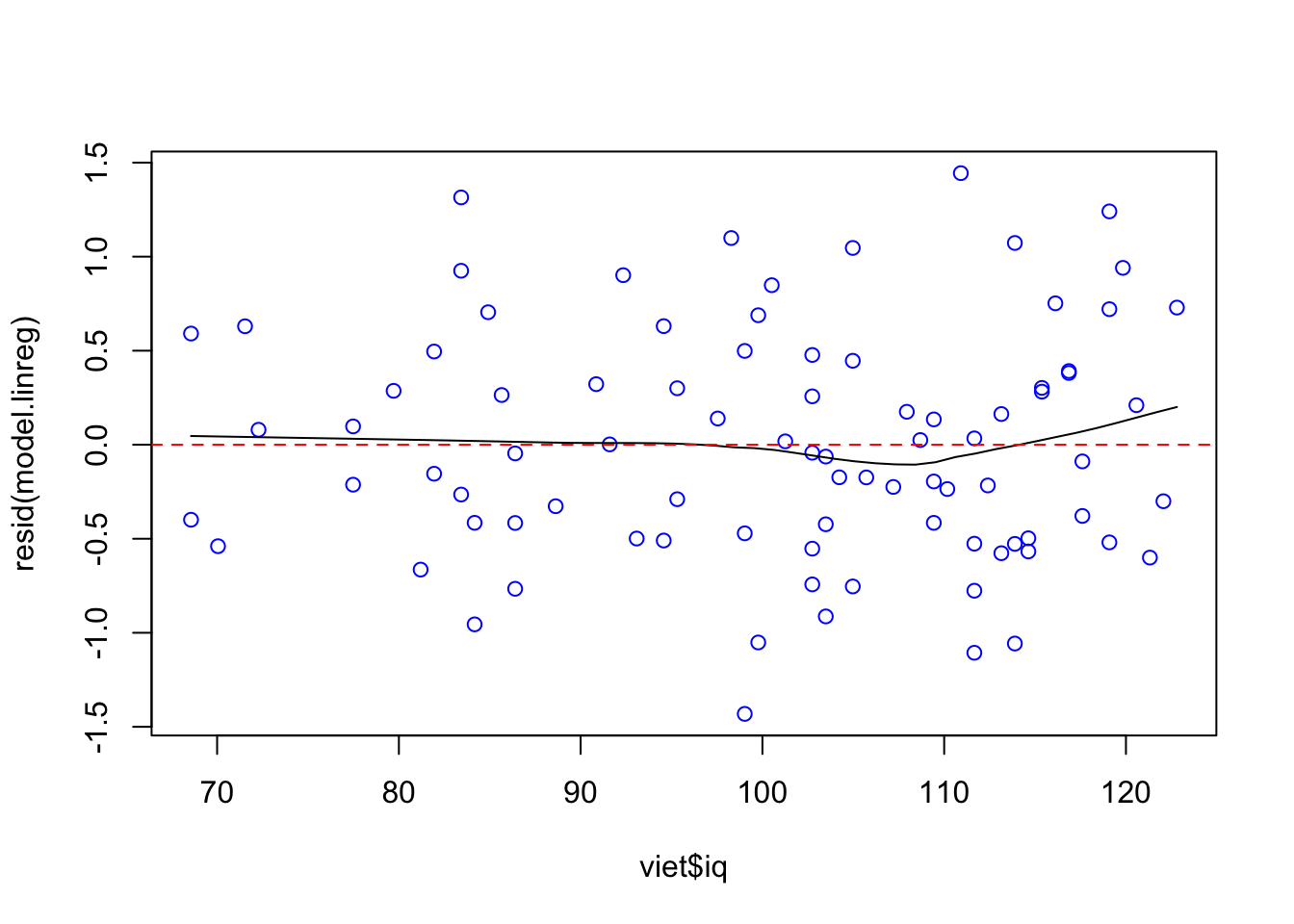
Vi ser efter, om den sorte linje laver for store udsving i forhold til den røde linje. Har vi flere kvantitative variable med i modellen, plotter vi residualerne mod dem alle enkeltvist.
5.7 Diagnostics
Eksempel Vitamin D (uge 5)
Modellen er:
vit$sol <- factor( ifelse( vit$sunexp=="Avoid sun", 0, 1 ))
lm4 <- lm( vitd ~ sol + bmi, data=vit )5.7.1 Cook’s afstand
Vi kan plotte Cook’s afstand mod f.eks. observationsnummeret for at se, hvem der evt har en stor afstand.
plot( lm4, which = 4 )
abline( 4/213, 0, col = "red", lty = 2)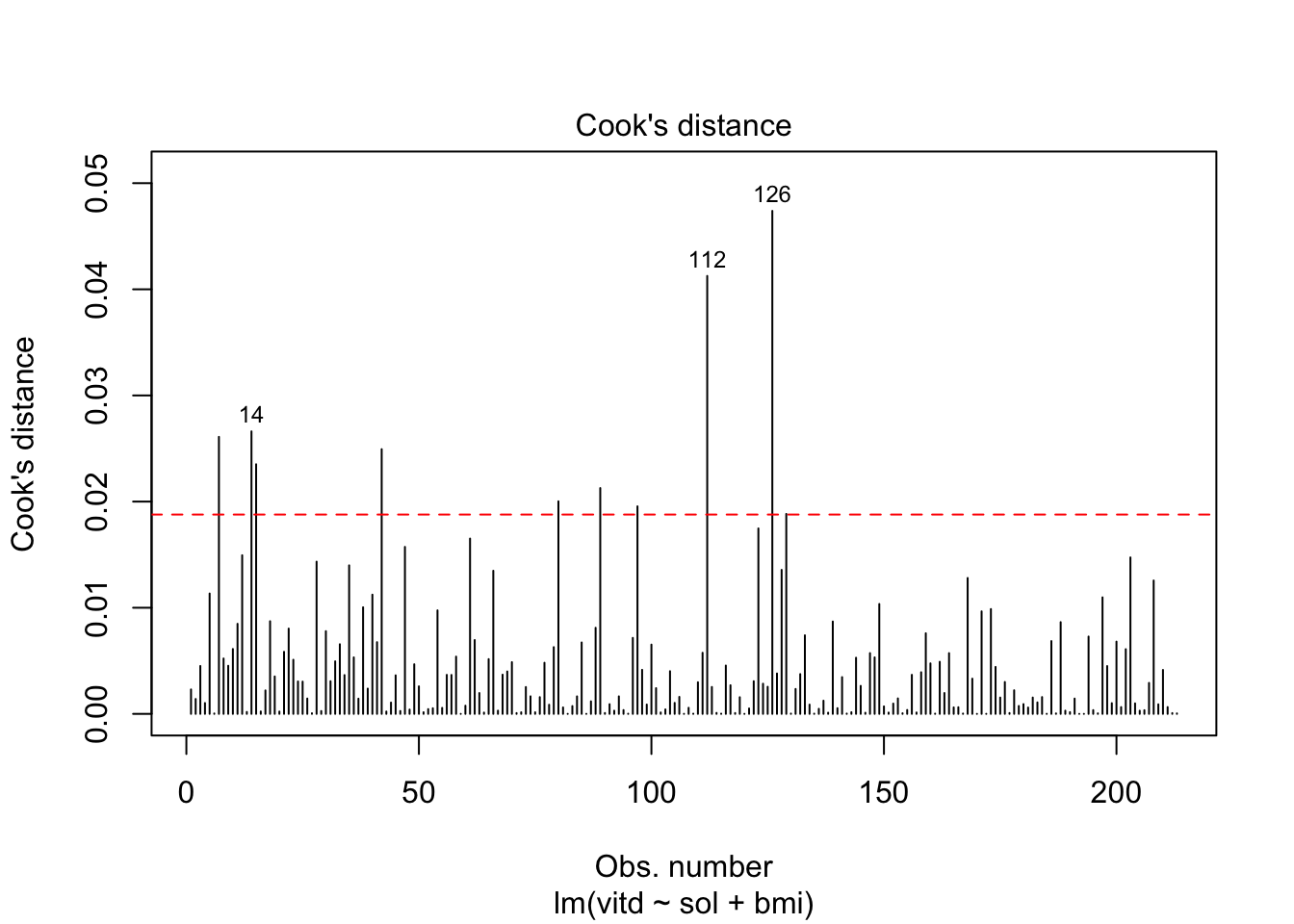
Som grænse for hvornår Cook er stor benyttes ofte \(4/n\).
Ønsker vi tallene for Cook’s distance frem for hvert individ kan vi gøre det med
cooks.distance( lm4 )(rund evt af til 2 decimaler for at få læsbart output, round( cooks.distance( model.linreg ), 2)
5.7.2 Influence
Influence er Cook’s afstand spaltet ud på de enkelte estimerede parametre (dvs intercept og hældninger) bestemmes ved hjælp af dfbetas().
dfbetas( lm4 )Som grænse for hvornår dfbeta er stor benyttes ofte \(2/\sqrt{n}\).
5.8 Prædiktion
Ud fra en lineær model kan vi lave prædiktioner. Det svarer til at vi beregner punkter på regressionslinjen. Det gøres ved først at definere et datasæt med den/de nye værdier vi ønsker at prædiktere for.
5.8.1 Model med én kovariat
Eksempel: Vietnam veteraner, IQ og lungefunktion.
Vi ønsker at prædiktere FEV1-niveau svarende til iq=100. Vi definerer derfor et nyt datasæt, som indeholder en kovariat med navnet iq, som skal have værdien 100:
nyedata <- data.frame(iq = 100)
nyedata iq
1 100Herefter kan vi bruge vores model model.linreg til at prædiktere værdien af FEV1 i vores nye ‘kunstige’ datasæt nyedata vha predict():
predict( model.linreg, newdata=nyedata) 1
3.945 WARNING: Man kan ikke få predict() til at virke hvis man er kommet til at benytte dollar-notation i sin model, dvs hvis man har kørt analysen a la lm( viet$FEV1 ~ viet$iq).
Vi estimerer altså at veteraner med en IQ på 100 har et niveau af FEV1 på 3.94L. Dette kan vi illustrere på følgende måde:
plot( viet$FEV1 ~ viet$iq)
abline( model.linreg )
pred <- predict( model.linreg, newdata=nyedata)
points( 100, pred, pch=20, col=2, cex=2 )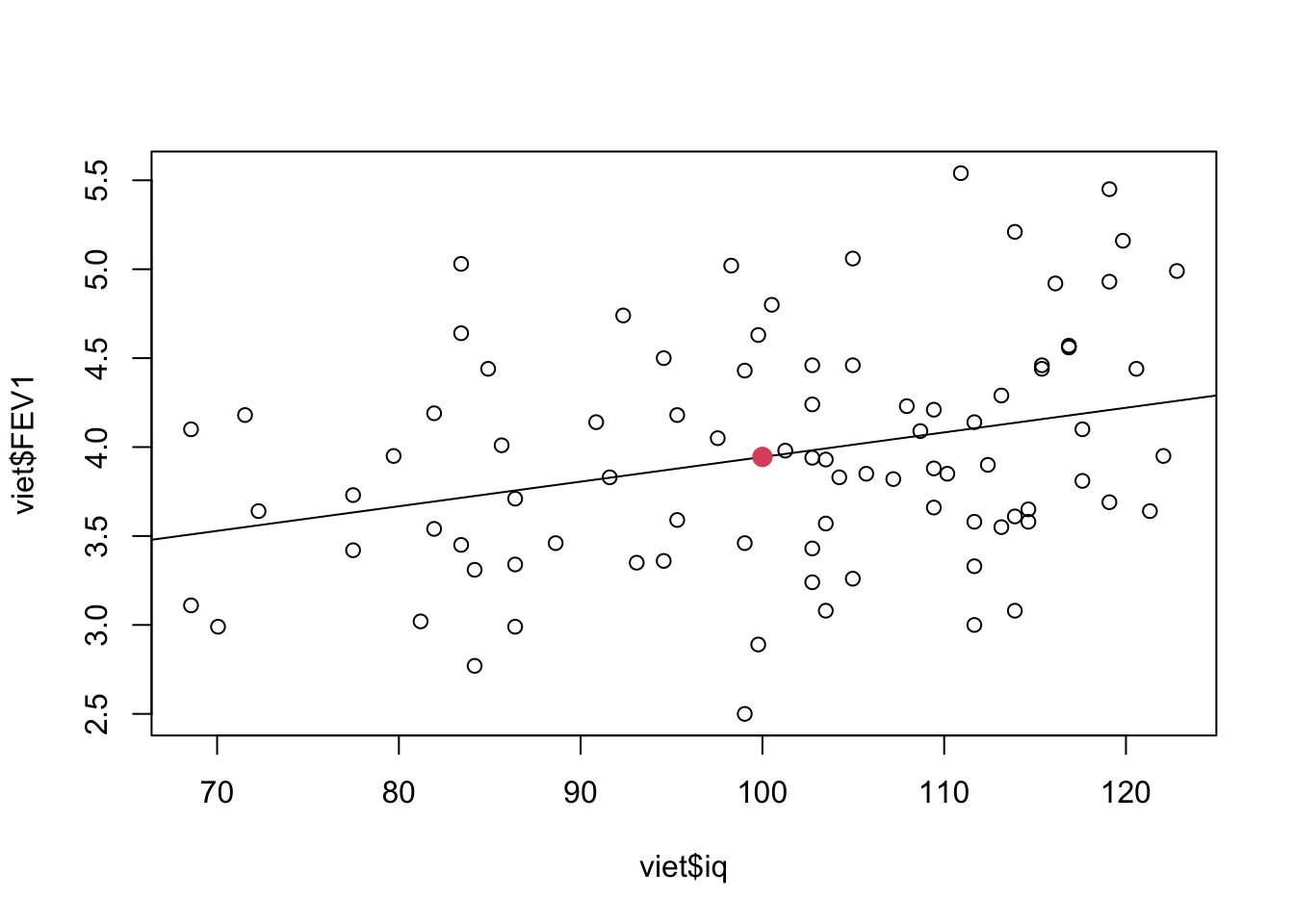
Vi kan lave prædiktionen incl CI vha et interval-argument:
predict( model.linreg, newdata=nyedata, interval = "confidence") fit lwr upr
1 3.945 3.812 4.077Her aflæses den prædikterede værdi under fit og konfidensintervallet under lwr og upr
Vi kan også lave prædiktionen incl prædiktionsinterval:
predict( model.linreg, nyedata, interval = "prediction")5.8.2 Plot af CI og prædiktionsgrænser
Vi kan konstruere en figur med konfidens- og prædiktionslinjer på nedenstående måde, som er lidt omstændig… Her skal man prædiktere for flere mulige værdier på x-aksen på en gang således at man kan få beregnet CI-og prædiktionsgrænserne omkring linjen (disse linjer er ikke rette linjer og skal derfor bestemmes for en fin inddeling af værdierne på x-aksen, så vi får pæne glatte krumme kurver, når vi plotter dem):
- Lav et nyt datasæt som indeholder værdier på x-aksen (her mulige værdier af
iq, fra 68 til 123)
nyedata <- data.frame( iq= 68:123 )
head( nyedata ) iq
1 68
2 69
3 70
4 71
5 72
6 73De mulige værdier her skal specificeres med et rimeligt fint interval (her er valgt en skridtstørrelse på 1), så vi får tegnet en fin glat kurve, når vi skal tegne de krumme kurver svarende til konfidensinterval omkring linjen.
- Beregn prædiktioner incl CI og prædiktionsinterval:
pred.plim <- predict( model.linreg, newdata=nyedata, interval = "prediction")
pred.clim <- predict( model.linreg, newdata=nyedata, interval = "confidence")Nu indeholder hhv pred.plim og pred.clim en matrix:
head( pred.clim ) fit lwr upr
1 3.501 3.170 3.832
2 3.515 3.193 3.837
3 3.529 3.215 3.843
4 3.543 3.237 3.848
5 3.557 3.259 3.854
6 3.570 3.281 3.860Første linje svarer til prædiktionen for første observation i vores nye datasæt nyedata, dvs iq=68. Anden række svarer til iq=69 etc. Der er således en række for hver værdi af iq i nyedata, dvs 56 (=nrow(nyedata)) linjer ialt. Søjle 1 indholder prædikterede værdier, søjle 2 nedre CI, søjle 3 øvre CI.
Når man vil hente værdierne i pred.clim og pred.plim kan man desværre ikke bruge dollar-notation (a la pred.clim$fit) men er nødt til at hive fat i søjlenummeret (a la pred.clim[ ,1] for at få søjle nr. 1).
- Plot. Vi plotter først observationerne incl regressionslinjen
plot( viet$FEV1 ~ viet$iq)
abline( model.linreg )og lægger derefter linjerne svarende til lwr og upr-søjlerne (hhv 2. og 3. søjle) oveni:
# Konfidensgrænser
lines( pred.clim[,2] ~ nyedata$iq, col="red", lty=2)
lines( pred.clim[,3] ~ nyedata$iq, col="red", lty=2)
# Prædiktionsgrænser
lines( pred.plim[,2] ~ nyedata$iq, col="blue", lty=3)
lines( pred.plim[,3] ~ nyedata$iq, col="blue", lty=3)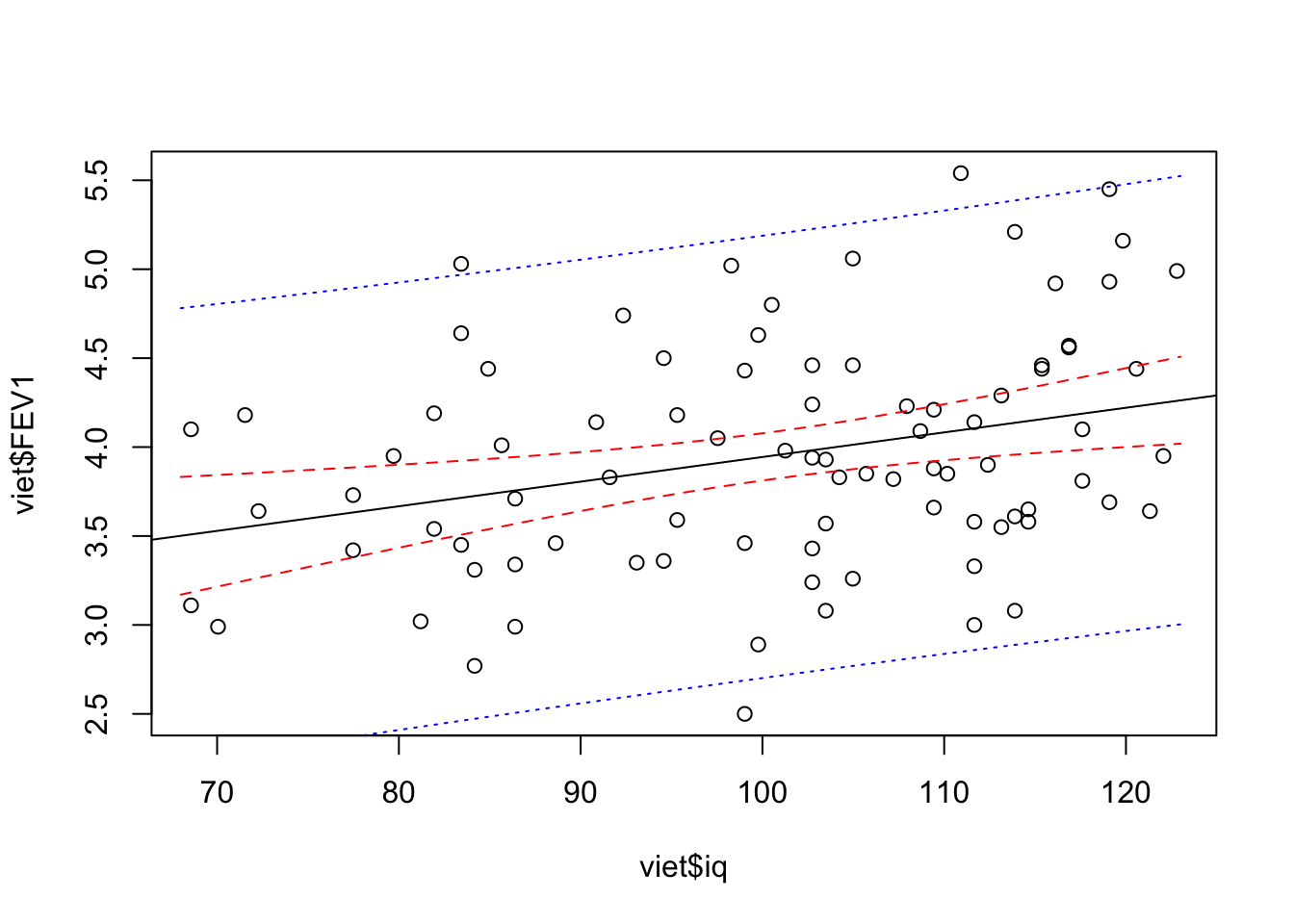
Her ser vi så at y-aksen er blevet for lille og vi derfor ikke får linjerne helt med og vi justerer derfor aksen og kører det hele en gang til
plot( viet$FEV1 ~ viet$iq, ylim=c(2,5.5))
abline( model.linreg )
# Konfidensgrænser
lines( pred.clim[,2] ~ nyedata$iq, col="blue", lty=2)
lines( pred.clim[,3] ~ nyedata$iq, col="blue", lty=2)
# Prædiktionsgrænser
lines( pred.plim[,2] ~ nyedata$iq, col="red", lty=3)
lines( pred.plim[,3] ~ nyedata$iq, col="red", lty=3)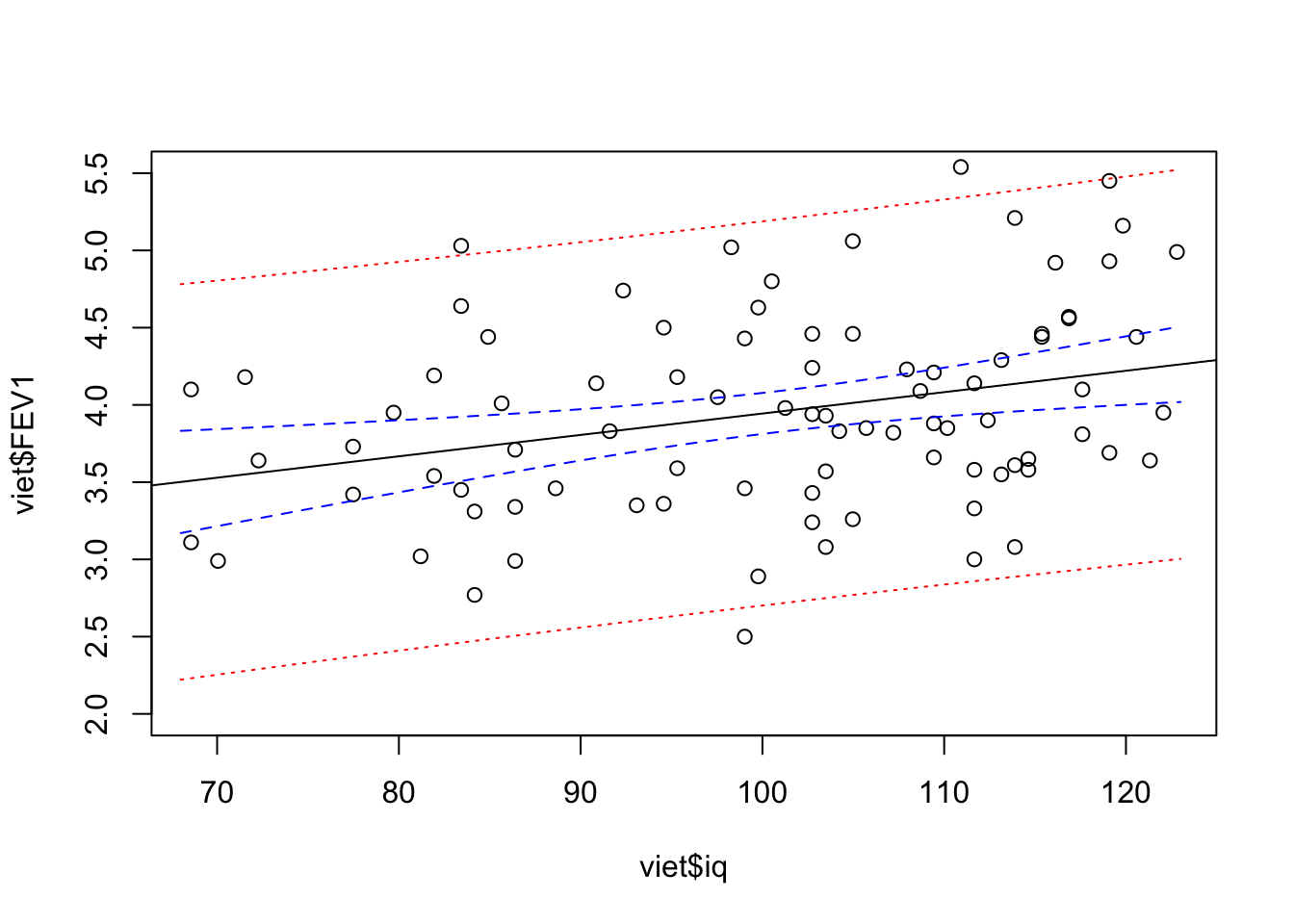
Avanceret: Man kan også benytte matplot() eller matlines() til at tegne mange linjer på en gang, men så skal man holde tungen lige i munden …
- Vi plotter først data,
FEV1som funktion afiq - Med
matlines()kan vi tilføje linjer, hvor y-værdierne er angivet i en søjle i en matrix (præcis som ipred.climogpred.plim). Linjerne (=søjlerne) plottes en af gangen og vi specificerer linjefarver og typer svarende til hver søjle:
plot( FEV1 ~ iq, data=viet, ylim=c(2,5.5))
matlines( nyedata$iq, pred.clim,
col = c("black","blue","blue"), lty = c(1,2,2))
matlines( nyedata$iq, pred.plim,
col = c("black","red","red"), lty = c(1,3,3))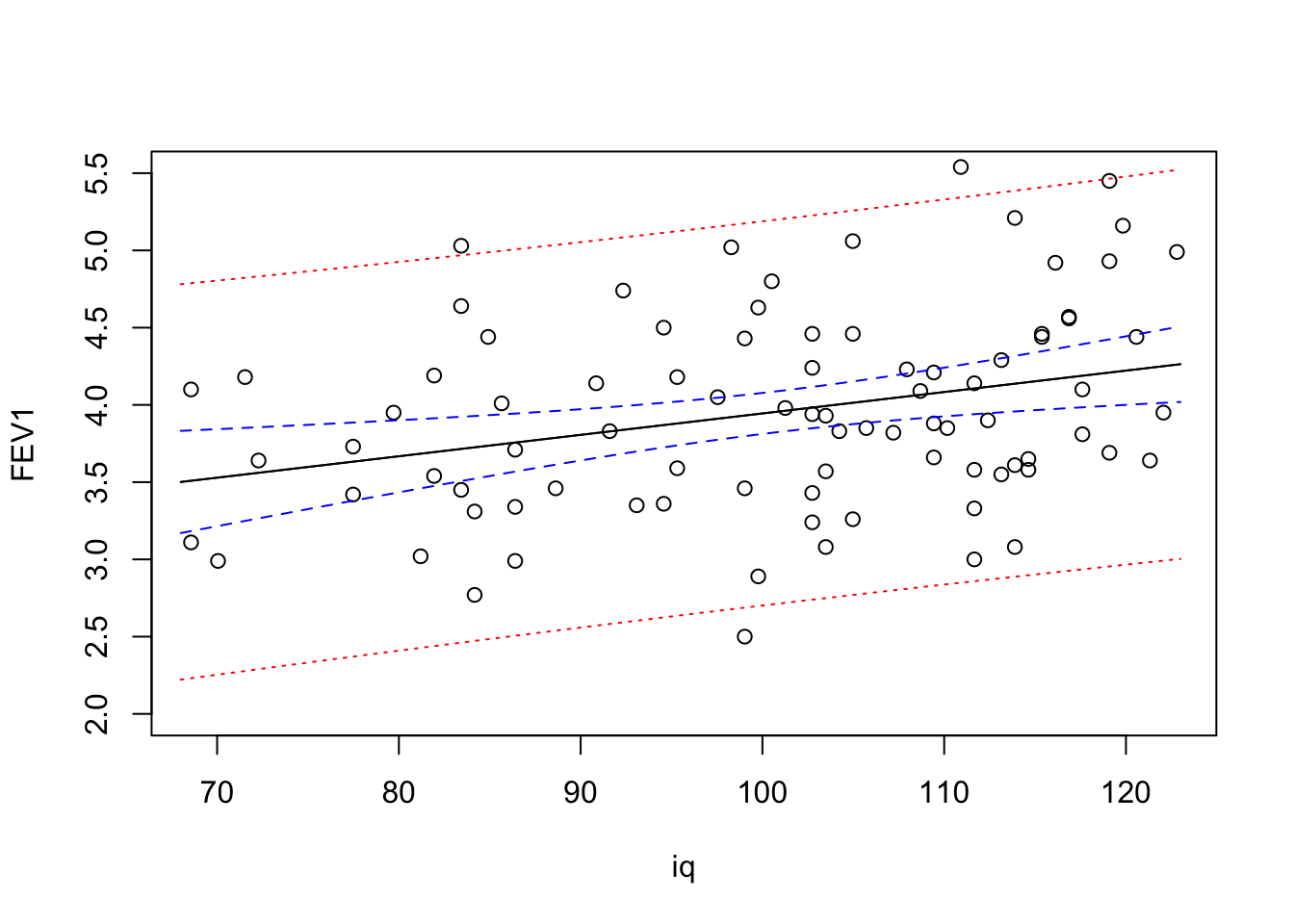
Bemærk at vi med denne fremgangsmåde egentligt tegner selve regressionslinjen (den sorte, fit to gange - en gang for hhv pred.clim og en gang for pred.plim, men når vi bruger samme farve / linjetype kan man selvføgelig ikke se det i plottet).
Med matplot() kan man starte med at tegne linjerne, lægge punkterne på bagefter - men det kan være farligt fordi man ikke opdager, hvis nogle punkter er så ekstreme at de kommer til at falde uden for plottet.
Her laver vi alle linjer i et hug ved at klistre pred.clim og pred.plim sammen til en matrix med 6 søjler med cbind() (Column BIND), og skal så tilsvarende huske 6 linjetyper og 6 farver. Samtidigt specificerer vi med type="l" at den skal tegne linjer, ikke punkter:
matplot(nyedata$iq, cbind(pred.clim, pred.plim),
lty = c(1,2,2,1,3,3), col = c("blue","blue","blue","blue","red","red"),
type = "l", ylab = "FEV1", xlab = "iq")
points(viet$iq, viet$FEV1)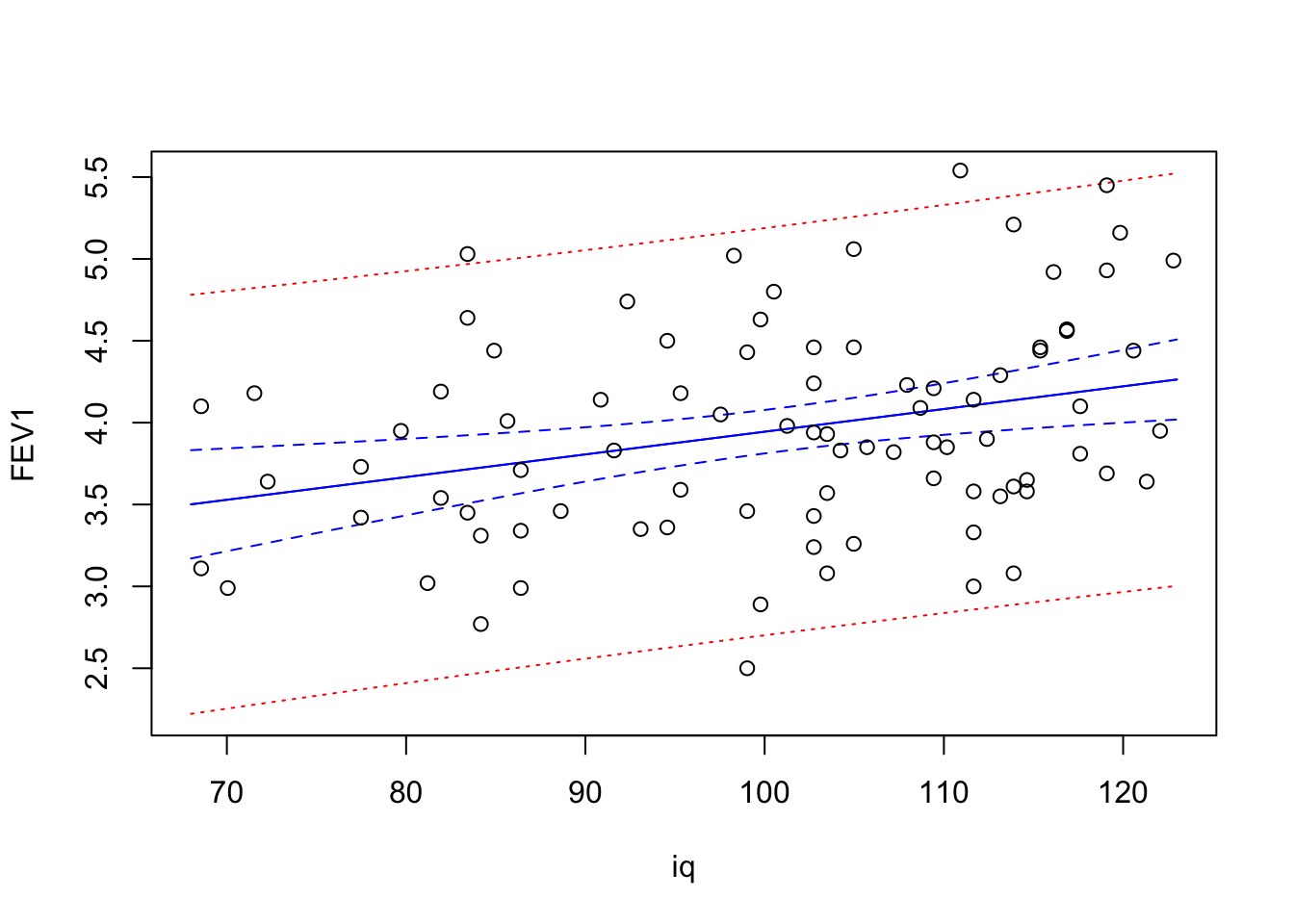
Voila! Og pyh …
5.8.3 Model med flere kovariater
Eksempel: AMH og p-piller (uge 5).
Vi vil prædiktere regressionslinjerne for hhv ikke-brugere og brugere af P-piller ud fra interaktionsmodellen:
interaktion = lm(logamh ~ alder + ppiller + ppiller:alder,
data = pill)Når vi skal prædiktere ud fra en multivariabel model skal vi definere et nyt datasæt, som indeholder prædiktionsværdier for alle kovariaterne i modellen. Disse værdier skal selvfølgelig stemme overens med de værdier, vi har set i vores datasæt, så vi ikke ekstrapolerer ud over det rimelige. Her er der to kovariater: alder og ppiller (og deres interaktion, men det behøver vi ikke specificere). Ønsker vi at prædiktere i ikke-P-pille-gruppen for aldre 20-45, kan vi specificere
ny0 <- data.frame( alder=20:45, ppiller=factor(0) )NB: Da ppiller er defineret som en faktor i vores datasæt pill skal det også være en faktor i prædiktionsdatasættet, ellers kan R ikke finde ud af det. I datasættet ny0 får alder værdierne 20 til 45, mens ppiller er 0 for alle.
Vi kan nu prædiktere for 20-45-årige ikke-brugere med:
predict( interaktion, ny0 )Tilsvarende kan vi gøre for brugerne (som jo så skal have ppiller=1), se nedenfor.
Vi kan plotte vores data (se R-script uge 5 for forklaringer om P-pille-specifikt plot- og farvesymbol (pch og col))
# Scatter plot af data
plot( pill$alder, pill$logamh,
main = "Analysis with Interaction",
ylab = "logamh", xlab = "alder",
pch = as.numeric( factor( pill$ppiller )),
col = as.numeric( factor( pill$ppiller )), cex.lab = 1.5)
legend('bottomright', legend = c(0,1),
pch = 1:2, col = 1:2, inset=.01)
# Prædiktionsdatasæt
ny0 <- data.frame( alder=20:45, ppiller=factor(0) )
ny1 <- data.frame( alder=20:45, ppiller=factor(1) )
# Tegner prædiktionerne for hver gruppe
lines( ny0$alder, predict( interaktion, ny0) )
lines( ny1$alder, predict( interaktion, ny1), col=2 )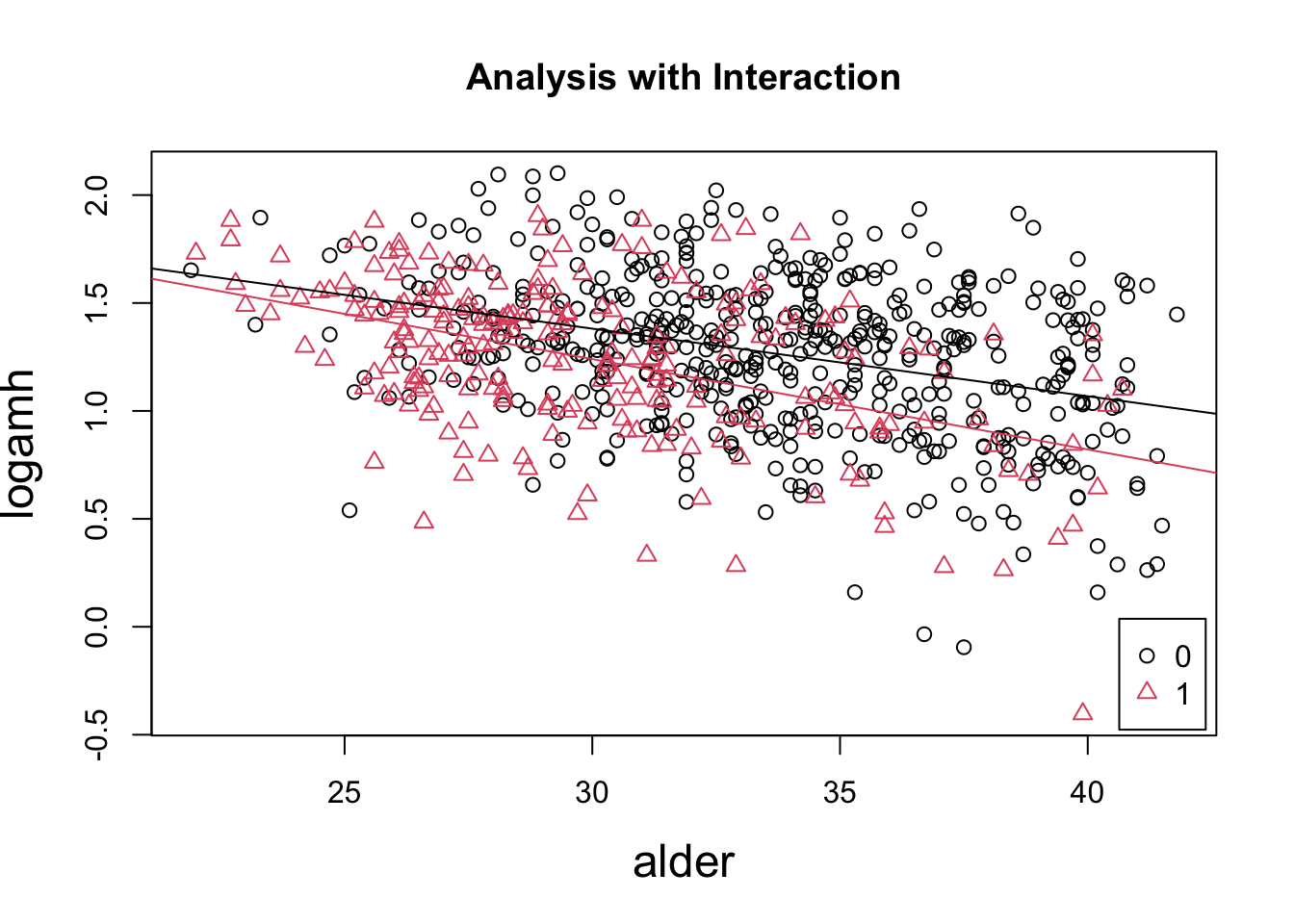
Øvelse: Hvis du har tid kunne du prøve at lægge CI omkring de to linjer ovenfor (se afsnit 5.8.2).
5.9 Kvantificering
Eksempel: AMH og p-piller (uge 5).
Vi kan regne videre på koefficienterne (=estimaterne), når vi har fittet en model. Her kan vi benytte glht() (General Linear Hypotheses Test) fra multcomp-pakken. I videoen nedenfor (20 min) viser jeg hvordan man kan regne videre på estimaterne i modellen med interaktion mellem p-piller og alder:
interaktion = lm(logamh ~ alder + ppiller + ppiller:alder,
data = pill)Videoen kan du finde her, hvis den ikke vises automatisk herunder.
Videoens indhold:
Jeg finder frem til linjens ligning for hver af de to P-pille-grupper:
- Ikke-brugere: 2.32 - 0.03*
alder - Brugere: 2.50 - 0.04*
alder
og viser hvordan man bestemmer CI for hældningen i hver gruppe vha glht():
library(multcomp)
# Hældning ikke-brugere
confint( summary( glht( interaktion, rbind(c(0,1,0,0))) ) )
# Hældning brugere
confint( summary( glht( interaktion, rbind(c(0,1,0,1))) ) )Dette kan man dog også gøre via en omparameterisering af modellen
interaktion2 = lm(logamh ~ ppiller + ppiller:alder -1,
data = pill)Vi kan beregne forskellige summer (linearkombinationer) af parametre og værdier, fx kan vi bestemme forskellen mellem brugere og ikke-brugere ved 25 og 40 år:
confint( summary( glht( interaktion, rbind(c(0,0,1,25))) ) )
confint( summary( glht( interaktion, rbind(c(0,0,1,40))) ) )
# og huske at regne tilbage til originalskala (=relativ forskel)
10^confint( summary( glht( interaktion, rbind(c(0,0,1,25))) ) )$confint
10^confint( summary( glht( interaktion, rbind(c(0,0,1,40))) ) )$confint5.10 Splines
Hvis en ikke-lineær sammenhæng ikke kan transformeres til linearitet (f.eks. ved log-transformation af kovariaten) kan man benytte spline-funktioner. Her findes forskellige varianter, den simpleste, som præsenteres her, er lineære splines. Her skæres en kurve op i stykkevis lineære bidder. Fordelene ved at bruge lineære splines i forhold til andre typer af splines er, at vi får en model som er let at rapportere - vi kan give en hældning i hvert af intervallerne.
I eksemplet med væksthormon som funktion af alder gennemgået i uge 7, lavede vi sammenhængen stykkevis lineær i intervaller < 10, 10-12, 12-13, 13-15, > 15 år, dvs kurven knækker ved 10, 12, 13 og 15 (svært at se knæk ved 10 og 12 år).
Bemærk at vi i eksemplet kun betragter en udvalgt del af datasættet og benytter kvadratrodstransformeret sigf1 som outcome:
juul.20 <- subset(juul, (age <= 20) & (age >= 5) & (sexnr==1))
juul.20$ssigf1 = sqrt(juul.20$sigf1)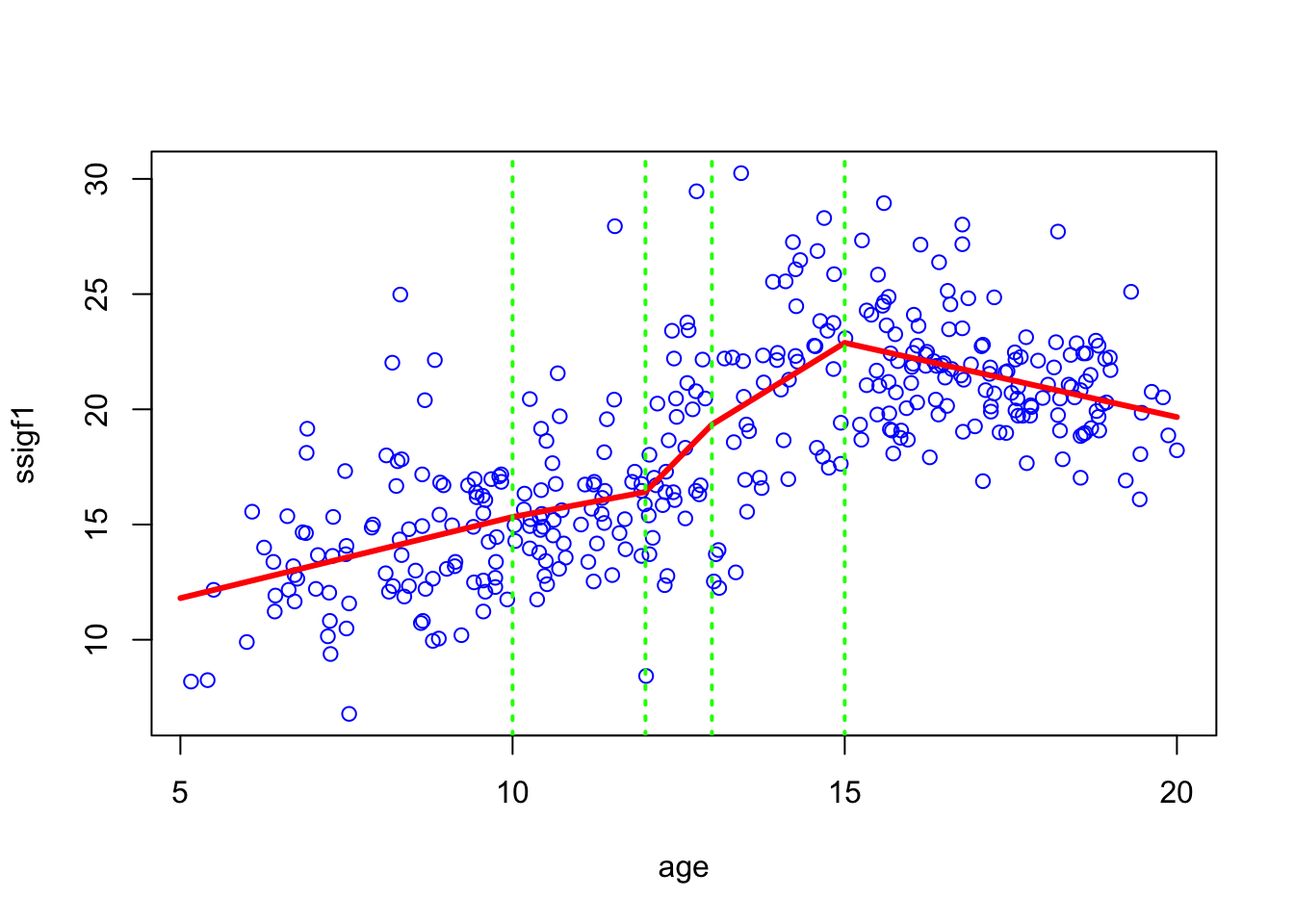
I praksis fittes en sådan kurve ved først at specificere knækpunkterne og derefter definere en spline-variabel for hvert tidspunkt:
juul.20$extra.age10 = pmax(juul.20$age - 10, 0)
juul.20$extra.age12 = pmax(juul.20$age - 12, 0)
juul.20$extra.age13 = pmax(juul.20$age - 13, 0)
juul.20$extra.age15 = pmax(juul.20$age - 15, 0)Disse benyttes derefter som kovariater i lm() sammen med den oprindelige variabel (her age):
model.spline <- lm(ssigf1 ~ age + extra.age10 + extra.age12 + extra.age13 + extra.age15, data = juul.20, na.action = na.exclude)Fortolkningen af spline-variablene er her: extra.age10 angiver forskellen i hældning i intervallet 10-12 ifht < 10, extra.age12 angiver forskellen i hældning i intervallet 12-13 ifht 10-12 etc.
Er alle disse forskelle i hældninger 0, dvs ingen effekt af splinevariablene, har vi kun age tilbage - og dermed linearitet.
Dette kan vi teste vha et anova, hvor vi tester vores spline-model mod en model uden vores spline-variable.
model.lin <- lm(ssigf1 ~ age, data = juul.20, na.action = na.exclude)
anova(model.spline, model.lin)Er der som i eksemplet her ikke linearitet (du finder en p-værdi for linearitet under ´Pr(>F)´), vil vi gerne rapportere hældningen i hvert interval frem for forskellen i hældninger mellem intervaller incl konfidensintervaller. Vi kan selvfølgelig nemt beregne hældningerne i hvert interval (ved at lægge koefficienterne sammen) ud fra vores summary - men vi kan ikke beregne konfidensintervaller i hånden.
Vi skal derfor have R til at lave beregningerne for os. Det kan vi enten gøre som vist i slides, ved at definere et sæt nye spline-variable ud fra de oprindelige spline-variable. Nemmere er det dog at benytte glht()-funktionen fra multcomp-pakken beskrevet i kapitel 5.9 ovenfor. Vi viser begge fremgangsmåder her:
** Bestemmelse af hældninger i hvert interval ud fra nye spline-variable**
De nye spline-variable defineres således ud fra de gamle:
ny_age10=pmin(extra_age10,2)ny_age12=pmin(extra_age12,1)ny_age13=pmin(extra_age13,2)ny_age15=extra_age15
Tallene 2, 1 og 2 benyttet i pmin-funktionerne angiver længden af intervallerne (her 12-10=2, 13-12=1, 15-13=2).
Derefter fittes en model med disse spline-variable i stedet:
# Nye spline-variable
juul.20$ny.age = pmin( juul.20$age, 10)
juul.20$ny.age10 = pmin( juul.20$extra.age10, 2)
juul.20$ny.age12 = pmin( juul.20$extra.age12, 1)
juul.20$ny.age13 = pmin( juul.20$extra.age13, 2)
juul.20$ny.age15 = juul.20$extra.age15
# Ny spline-model
model.spline2 <- lm(ssigf1 ~ ny.age + ny.age10 + ny.age12 + ny.age13 + ny.age15, data = juul.20)
summary(model.spline2)
confint(model.spline2)** Bestemmelse af hældninger i hvert interval ved brug af glht()**
Vi tager først et kig på estimaterne:
coef( model.spline )og ser heraf at vi har ialt 6 koefficienter i modellen ((Intercept),age,extra.age10, extra.age12, extra.age13 og extra.age15)
- Her svarer koefficient nr 2 (
age) til hældningen i første interval (alder < 10 år) - Summen af koefficient nr 2 og 3 (
ageogextra.age10) er hældningen i andet interval (alder 10-12 år) - etc.
Der er ialt 6 koefficienter i vores model. Vi kan plukke 2. og 3. element ud og lægge dem sammen ved at benytte notation c(0,1,1,0,0,0) i glht() som beskrevet i kapitel @ref(#kvant) ovenfor:
# < 10 (svarende til koefficient til alder)
confint( glht( model.spline, linfct=rbind(c(0,1,0,0,0,0))) )
# 10-12
confint( glht( model.spline, linfct=rbind(c(0,1,1,0,0,0))) )
# 12-13
confint( glht( model.spline, linfct=rbind(c(0,1,1,1,0,0))) )
# 13-15
confint( glht( model.spline, linfct=rbind(c(0,1,1,1,1,0))) )
# > 15
confint( glht( model.spline, linfct=rbind(c(0,1,1,1,1,1))) )5.11 Test af flere parametre
Eksempel: Vitamin d uge 7, den generelle lineære model.
Vi kan teste vilkårlige kombinationer af parametrene lig 0 i et overordnet test på to måder:
* vha en F-test som laves med anova-funktionen, hvis det er hele variable der fjernes fra modellen
* vha glht-funktionen, hvor man manuelt kan specificere en kombination af parametre som man vil teste om er 0
I eksemplet gennemgået i forelæsningerne ønsker vi at teste, om der samlet set er effekt af bmi, sunexp og lvitdintake på log-transformeret vitamin D (log2vitd), justeret for country. Vi spørger altså om vi kan udelade disse tre variable og kun beholde country i modellen. Til dette kan vi benytte anova().
Først log-transformerer vi de variable, vi skal bruge i transformeret form. Hvorefter vi definere den store model med alle kovariater og den lille model vi vil teste mod, hvor 3 variable er udeladt.
vit$log2vitd <- log2(vit$vitd)
vit$lvitdintake <- log2(vit$vitdintake)
model3 = lm(log2vitd ~ bmi + relevel(sunexp, ref="Sometimes in sun") + lvitdintake + relevel(country, ref = "SF"),
data = vitd2, na.action = na.exclude)
model1 = lm(log2vitd ~ relevel(country, ref="SF"), data = vit, na.action = na.exclude)
anova(model3, model1)Her aflæses p-værdien for F-testen under Pr(>F).
5.12 Korrelation
Korrelation kan bestemmes mellem to kvantative variable.
Der findes flere typer korrelation:
- Pearson korrelationen: Bygger på antagelse om to-dimensionel normalfordeling
- Spearman korrelationen: Kræver kun tilfældig udvælgelse af 2-dimensionel fordeling (ikke nødvendigis normalfordeling)
# Pearson
cor.test(viet$iq, viet$FEV1)
# Spearman
cor.test(viet$iq, viet$FEV1, method="spearman")
# Kendall
cor.test(viet$iq, viet$FEV1, method="kendall")NB: Beregner man Spearman korrelationen får man en warning:
Advarselsbesked:
I cor.test.default(viet$iq, viet$FEV1, method = "spearman") :
Cannot compute exact p-value with tiesDer er “ties” i data, når nogle observationer har samme værdi. Feks er der to veteraner som har den lavest observerede værdi på 68.56. Det betyder, at vi ikke får beregnet p-værdien helt præcist. Den kan I se stort på, så længe I ikke har et meget lille datasæt / meget få værdier af den ene variabel.